Hvordan finne asymptoter av en hyperbola
 Share
Share
hyperbelen
Hyperbola er en konisk del. Begrepet hyperbola refereres til de to frakoblede kurvene som er vist i figuren.
Hvis hovedaksene er sammenfallende med de kartesiske aksene, er den generelle ligningen av hyperbola av formen:

Disse hyperbolaene er symmetriske rundt y-aksen og er kjent som y-akse-hyperbola. Hyperbola-symmetrisk rundt x-akse (eller x-akse-hyperbola) er gitt av ligningen,
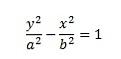 Hvordan finne asymptotene til en hyperbola
Hvordan finne asymptotene til en hyperbola
For å finne asymptotene til en hyperbola, bruk en enkel manipulering av ligningen til parabolen.
Jeg. Først legg parabolas likning til over gitt form
Hvis parabolen er gitt som mx2+ny2=l, ved å definere
en= √ (l/m) og b= √ (-l/n) hvor l<0
(Dette trinnet er ikke nødvendig hvis ligningen er gitt i standard fra.

ii. Deretter erstatter høyre side av ligningen med null.

iii. Faktoriser ligningen og ta løsninger

Derfor er løsningene ,

Likninger av asymptotene er

Likninger av asymptotene for x-aksen hyperbola kan også oppnås ved samme fremgangsmåte.
Finn asymptotene til en hyperbola - Eksempel 1
Tenk på hyperbola gitt av ligningen x2/ 4-y2/ 9 = 1. Finn ligningene til asymptotene.

Skriv om ligningen og følg fremgangsmåten ovenfor.
x2/ 4-y2/ 9 = x2/ 22 -y2/ 32 = 1
Ved å erstatte høyre side med null blir ligningen x2/ 22 -y2/ 32 = 0.
Faktorisering og oppløsning av ligningen gir,
(X / 2-y / 3) (x / 2 + y / 3) = 0
Likninger av asymptotene er,
3x-2y = 0 og 3x + 2y = 0
Finn asymptotene til en hyperbola - Eksempel 2
- Ligning av en parabola er gitt som -4x² + y² = 4

Denne hyperbola er en x-akse hyperbola.
Omarrangere betingelsene til hyperbola i standarden fra gir
-4x2+ y2= 4 => y2/ 22 -x2/12 = 1
Faktorisering av ligningen gir følgende
(Y / 2-x) (y / 2 + x) = 0
Derfor er løsningene y-2x = 0 og y + 2x = 0.
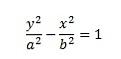 Hvordan finne asymptotene til en hyperbola
Hvordan finne asymptotene til en hyperbola 