Forskjellen mellom T-test og ANOVA
 Share
Share
 Det er en tynn linje av avgrensning mellom t-test og ANOVA, dvs. når populasjonsmidler av bare to grupper skal sammenlignes, t-test brukes, men når det skal sammenlignes med mer enn to grupper, ANOVA er foretrukket.
Det er en tynn linje av avgrensning mellom t-test og ANOVA, dvs. når populasjonsmidler av bare to grupper skal sammenlignes, t-test brukes, men når det skal sammenlignes med mer enn to grupper, ANOVA er foretrukket.
T-test og Variansanalyse forkortet som ANOVA, er to parametriske statistiske teknikker som brukes til å teste hypotesen. Da disse er basert på den felles antagelsen som at befolkningen fra hvilken prøven er tegnet, skal distribueres normalt, homogenitet av varians, tilfeldig prøvetaking av data, observasjonens uavhengighet, måling av den avhengige variabelen på forholdet eller intervallnivået, misforstår folk ofte disse to.
Her er en artikkel presentert for deg å forstå den betydelige forskjellen mellom t-test og ANOVA, ta en titt.
Innhold: T-test Vs ANOVA
Sammenligningstabel
| Grunnlag for sammenligning | T-test | ANOVA |
|---|---|---|
| Betydning | T-test er en hypotesetest som brukes til å sammenligne middelene til to populasjoner. | ANOVA er en statistisk teknikk som brukes til å sammenligne midlene til mer enn to populasjoner. |
| Test statistikk | (x ̄-μ) / (s / √n) | Mellom utvalgsvariasjon / innenfor utvalgsvariant |
Definisjon av T-test
T-testen er beskrevet som den statistiske testen som undersøker hvorvidt populasjonsmiddelene til to prøver er i stor grad forskjellig fra hverandre ved bruk av t-distribusjon som brukes når standardavviket ikke er kjent, og prøven er liten. Det er et verktøy for å analysere om de to prøvene trekkes fra samme befolkning.
Testen er basert på t-statistikk, som forutsetter at variabelen er normalt fordelt (symmetrisk klokkeformet fordeling) og gjennomsnitt er kjent og populasjonsvariancen beregnes fra prøven.
I t-test tar nullhypotesen form av H0: μ (x) = μ (y) mot alternativ hypotese H1: μ (x) ≠ μ (y), hvor μ (x) og μ (y) representerer populasjonsinnretningene. Graden av frihet til t-test er n1 + n2 - 2
Definisjon av ANOVA
Variansanalyse (ANOVA) er en statistisk metode som ofte brukes i alle situasjoner der det skal foretas en sammenligning mellom mer enn to populasjoner, som avkastningen av avlingen fra flere frøvarianter. Det er et viktig analyseverktøy for forskeren som gjør at han kan utføre test samtidig. Når vi bruker ANOVA, antas det at prøven trekkes fra den normalt distribuerte befolkningen og populasjonsvariancen er like.
I ANOVA er den totale mengden av variasjon i et datasett delt i to typer, dvs. mengden tildelt til sjanse og mengde tilordnet bestemte årsaker. Dens grunnleggende prinsipp er å teste avvikene mellom populasjonsmidler ved å vurdere mengden av variasjon innenfor gruppeposter, i forhold til mengden av variasjon mellom grupper. Innenfor prøven er variansen på grunn av den tilfeldige uforklarlige forstyrrelsen, mens forskjellig behandling kan medføre mellom utvalgsvarianter.
Ved bruk av denne teknikken tester vi null-hypotesen (H0) hvor alle populasjonsmidler er de samme, eller alternative hypoteser (H1) hvor minst en populasjonsmiddel er forskjellig.
Viktige forskjeller mellom T-test og ANOVA
De signifikante forskjellene mellom T-test og ANOVA er diskutert i detalj i følgende punkter:
- En hypotesetest som brukes til å sammenligne middel til to populasjoner kalles t-test. En statistisk teknikk som brukes til å sammenligne midlene til mer enn to populasjoner, kalles Analyse av Varians eller ANOVA.
- Teststatistikk for T-test er:
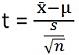 Teststatistikk for ANOVA er:
Teststatistikk for ANOVA er: 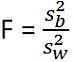
Konklusjon
Etter å ha gjennomgått de ovennevnte punktene, kan det sies at t-test er en spesiell type ANOVA som kan brukes når vi bare har to populasjoner for å sammenligne deres midler. Selv om muligheten for feil kan øke dersom t-test brukes når vi må sammenligne mer enn to midler til populasjonene samtidig, er det derfor ANOVA brukes
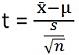 Teststatistikk for ANOVA er:
Teststatistikk for ANOVA er: