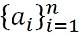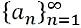Forskjellen mellom sekvens og serie

I matematikk og statistikk er linjen som avgrenser sekvens og serie tynn og sløret, på grunn av hvilken mange tror at disse begrepene er en og samme. Ikke desto mindre er begrepet sekvens forskjellig fra serier i den forstand at sekvens refererer til et arrangement i den spesielle rekkefølge der relaterte termer følger hverandre, dvs. den har en identifisert første enhet, andre enhet, tredje enhet og så videre.

Når en sekvens følger en bestemt regel, kalles den som progresjon. Det er ikke akkurat det samme som serie som er definert som summen av elementene i en sekvens. Ta en les av artikkelen for å vite den betydelige forskjellen mellom sekvens og serie.

Innhold: Sequence Vs Series

Sammenligningstabel

Grunnlag for sammenligning	Sekvens	Serie
Betydning	Sekvens beskrives som settet med tall eller objekter som følger et bestemt mønster.	Serien refererer til summen av elementene i sekvensen.
Rekkefølge	Viktig	Noen ganger viktig
Eksempel	1, 3, 5, 7, 9, 11 ... n ...	1 + 3 + 5 + 9 + 11 ... n ...

Definisjon av sekvens

I matematikk, et ordnet sett med objekter eller tall, som a₁, en₂, en₃, en₄, en₅, en₆... a_{n ... .}sies å være i en sekvens, dersom det, som per bestemt regel, har en bestemt verdi. Medlemmene av sekvensen kalles term eller element som er lik alle verdier av det naturlige tallet. Hvert sikt i en sekvens er relatert til foregående og etterfølgende sikt. Generelt har sekvenser skjulte regler eller mønster, noe som hjelper deg med å finne ut verdien av neste semester.

Det neste begrepet er funksjonen av heltal n (positiv), betraktet som den generelle termen av sekvensen. En sekvens kan være endelig eller uendelig.

Finite Sequence: En endelig sekvens er en som stopper på slutten av listen over tall a₁, en₂, en₃, en₄, en₅, en₆... a_n, er representert av:
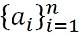
Uendelig sekvens: En uendelig sekvens refererer til en sekvens som er uendelig, a₁, en₂, en₃, en₄, en₅, en₆... a_{n ... .}., er representert av:

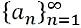
Definisjon av serie

Tillegg av betingelsene i en sekvens (a_n), er kjent som serie. Serien kan som sekvens også være finite eller uendelig, der en endelig serie er en som har et begrenset antall ord som er skrevet som en₁+ en₂+ en₃ + en₄+ en₅ + en_{6 +}... a_n. I motsetning til uendelig serie, hvor antall elementer ikke er uendelige eller som er uendelige, skrevet som en₁+ en₂+ en₃ + en₄+ en₅ + en_{6 +}... a_n+_{... .}

Hvis en₁+ en₂+ en₃ + en₄+ en₅ + en_{6 +}... a_n = S_n, så S_n regnes som summen til n elementer i serien. Summen av termer er ofte representert ved gresk bokstav sigma (Σ). derav,

Nøkkelforskjeller mellom sekvens og serie

Forskjellen mellom sekvens og serie kan tegnes tydelig av følgende grunner:

Sekvensen er definert som samling av tall eller objekter som følger et bestemt mønster. Når elementene i sekvensen blir lagt sammen, er de kjent som serier.
Bestem saker i en sekvens, da det er en viss regel som foreskriver mønsteret til sekvensen. Derfor er 1, 2, 3three forskjellig fra 3, 1, 2. På den annen side, i rekkefølge av utseende kan eller ikke er noe som helst, som i tilfelle av absolutt konvergente serier, betyr ordren ingen rolle. Så, 1 + 2 + 3 er det samme som 3 + 1 + 2, bare deres sekvens er forskjellig.

Konklusjon

Aritmetisk Progression (A.P.) og Geometrisk Progression (G.P.) er også sekvenser, ikke serier. Aritmetisk Progresjon er en sekvens der det er en felles forskjell mellom de påfølgende vilkårene som 2, 4, 6, 8 og så videre. Tvert imot, i en geometrisk progresjon, er hvert element i sekvensen det felles flertallet av det foregående uttrykk som 3, 9, 27, 81 og så videre. På samme måte er Fibonacci Sequence også en av de populære uendelige sekvensene, hvor hvert begrep er oppnådd ved å legge opp de to foregående vilkårene 1, 1, 3, 5, 8, 13, 21 og så videre.

utdanning