Forskjellen mellom middel og median
 Share
Share
 Sentral tendens innebærer at datapunktene har en tendens til å klare seg rundt sin sentrale eller mellomstore verdi. De to mest brukte tiltakene av sentral tendens er middel og median. Mener er definert som den "sentrale" verdien av det angitte datasettet mens median er "middelmest" -verdien i det angitte datasettet.
Sentral tendens innebærer at datapunktene har en tendens til å klare seg rundt sin sentrale eller mellomstore verdi. De to mest brukte tiltakene av sentral tendens er middel og median. Mener er definert som den "sentrale" verdien av det angitte datasettet mens median er "middelmest" -verdien i det angitte datasettet.
Et ideelt mål for sentral tendens er en som er klart definert, lett forståelig, bare kalkulerbar. Den skal være basert på alle observasjoner og minst berørt av ekstreme observasjoner i datasettet.
Folk kontrast ofte disse to tiltakene, men faktum er at de er forskjellige. Denne artikkelen fremhever spesielt de grunnleggende forskjellene mellom gjennomsnitt og median. Ta en titt.
Innhold: Betyd Vs Median
Sammenligningstabel
| Grunnlag for sammenligning | Mener | median |
|---|---|---|
| Betydning | Mean refererer til det enkle gjennomsnittet av det gitte settet av verdier eller mengder. | Median er definert som midtnummeret i en bestilt liste over verdier. |
| Hva er det? | Det er et aritmetisk gjennomsnitt. | Det er posisjonelt gjennomsnitt. |
| representerer | Datasettets tyngdepunkt | Datasettets tyngdepunkt Midtpunkt av datasett |
| Gyldighet | Normal distribusjon | Skewed distribusjon |
| uteliggere | Mean er følsom for utelukker. | Median er ikke følsom for utelukker. |
| beregning | Gjennomsnitt beregnes ved å legge opp alle observasjonene og deretter dele verdien oppnådd med antall observasjoner. | For å beregne median er datasettet ordnet i stigende eller synkende rekkefølge, så er verdien som faller i den eksakte midten av det nye datasettet, median. |
Definisjon av betydning
Middelet er det mye brukte målet for sentral tendens, som defineres som gjennomsnittet av settet av verdier. Den representerer modellen og den vanligste verdien av det oppgitte verdiområdet. Det kan beregnes, både i diskrete og kontinuerlige serier.
Gjennomsnittet er lik summen av alle observasjoner dividert med antall observasjoner i datasettet. Hvis verdien som antas av en variabel er lik, vil dens gjennomsnitt også være det samme. Middel kan være av to typer, prøven betyr (x)) og populasjonsmiddel (μ). Det kan beregnes med gitt formel:
- Aritmetisk gjennomsnitt:
 hvor Σ = gresk bokstav sigma, betegner sum av ...
hvor Σ = gresk bokstav sigma, betegner sum av ...
n = antall verdier - For diskret serie:
 hvor, f = frekvens
hvor, f = frekvens - For kontinuerlig servietter:
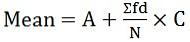 hvor d = (X-A) / C
hvor d = (X-A) / C
A = antatt middel
C = Felles divisor
Definisjon av median
Medianen er et annet viktig mål for sentral tendens, som brukes til å skille verdier i to like deler, dvs. større halvdel av prøven, befolkning eller sannsynlighetsfordeling fra den nedre halvdel. Det er middelverdien, som oppnås når observasjonene blir sortert i en bestemt rekkefølge, enten stigende eller synkende rekkefølge.
For beregning av medianen, først og fremst, ordne observasjonene i laveste til høyeste eller høyeste til laveste, og bruk deretter den riktige formelen, slik vilkårene er gitt nedenfor:
- Hvis antall observasjoner er merkelige:
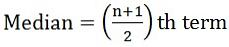 hvor n = antall observasjoner
hvor n = antall observasjoner - Hvis antall observasjoner er til og med:
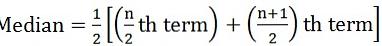
- For kontinuerlig serie:
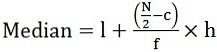 hvor, l = nedre grense for median klassen
hvor, l = nedre grense for median klassen
c = kumulativ frekvens for foregående median klasse
f = frekvens av median klassen
h = klasse bredde
Nøkkelforskjeller mellom middel og median
De betydelige forskjellene mellom gjennomsnitt og median er gitt i artikkelen nedenfor:
- I statistikk defineres et middel som det enkle gjennomsnittet av det gitte settet av verdier eller mengder. Medianen sies å være midtnummeret i en bestilt liste over verdier.
- Mens gjennomsnitt er det aritmetiske gjennomsnittet, er medianen posisjonelt gjennomsnitt, i hovedsak bestemmer datasettets posisjon verdien av medianen.
- Mean skisserer tyngdepunktet for datasettet mens median fremhever den midterste verdien av datasettet.
- Gjennomsnittet er passende for normalt distribuerte data. På den andre enden er medianen best når datafordelingen er skjev.
- Middelet er sterkt påvirket av ekstreme verdien som ikke er tilfelle med en median.
- Gjennomsnittet beregnes ved å legge opp alle observasjonene og deretter dele verdien oppnådd med antall observasjoner; resultatet er gjennomsnittlig. I motsetning til medianen er datasettet arrangert i stigende eller synkende rekkefølge, da er verdien som faller i den eksakte midten av det nye datasettet, median.
Eksempel
Finn gjennomsnittet og medianen til det angitte settet av data:
58, 26, 65, 34, 78, 44, 96
Løsning: For å beregne gjennomsnitt må du dele summen av observasjoner med antall observasjoner,

 Mean = 57,28
Mean = 57,28
For å beregne medianen, først og fremst, ordne serien i en sekvens, dvs. lavest til høyest,
26, 34, 44, 58, 65, 78, 96
 hvor n = antall observasjoner
hvor n = antall observasjoner
Konklusjon
Etter å ha gjennomgått de ovennevnte punktene, kan vi si at disse to matematiske konseptene er forskjellige. Aritmetisk middel eller Gjennomsnitt anses som det beste målet for sentral tendens, da den inneholder alle funksjonene til et ideelt mål, men det har en ulempe at samplingsfluktuasjonene påvirker gjennomsnittet.
På samme måte er medianen også entydig definert og lett å forstå og regne ut, og det beste med dette tiltaket er at det ikke påvirkes av samplingfluktuasjoner, men den eneste ulempen ved medianen er at den ikke er basert på alle observasjoner. For åpen endeklassifisering er medianen vanligvis foretrukket over gjennomsnittet.
 hvor Σ = gresk bokstav sigma, betegner sum av ...
hvor Σ = gresk bokstav sigma, betegner sum av ... hvor, f = frekvens
hvor, f = frekvens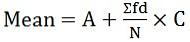 hvor d = (X-A) / C
hvor d = (X-A) / C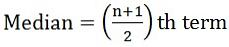 hvor n = antall observasjoner
hvor n = antall observasjoner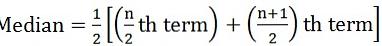
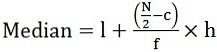 hvor, l = nedre grense for median klassen
hvor, l = nedre grense for median klassen Median = 4th term = 58
Median = 4th term = 58