Hvordan å beregne halveringstid
 Share
Share
I dette avsnittet vil vi lære om halveringstid og utlede formelen for å beregne halveringstid. I radioaktivitet, halvt liv er tiden som er tatt av halvparten av radioaktive kjerner i en prøve av en radioaktiv isotop til henfall. Antallet radioaktive kjerne i en prøve faller eksponentielt over tid. For å beregne halveringstid brukes derfor matematikken til eksponentiell forfall. Halvlivet er et ekstremt viktig konsept for bruk av radioaktivitet. Radioisotoper introdusert til organer i strålebehandling, for eksempel, må ikke ligge lenge i en pasients kropp. På den annen side må isotoper som brukes til å danse historiske gjenstander, ha lange halve liv, slik at nok av dem har blitt igjen til i dag for oss å bestemme objekternes alder.
Forskjellen mellom tilfeldig og spontan art av radioaktivt forfall
Radioaktivt henfall er kategorisert som begge deler tilfeldig og spontan.
- Radioaktivt henfall er tilfeldig fordi vi ikke kan bestemme når en gitt kjerne vil forfalle, eller bestemme hvor lang tid det ville ta før en gitt kjernen ville forfallne. Følgelig har hver radioaktive kjerne i en prøve den samme sannsynlighet for forfall på en gitt tid.
- Radioaktivt henfall er spontant fordi det ikke påvirkes av eksterne forhold.
Hva er Half Life
Antallet av radioaktive kjerne i en prøve faller, fordi når kjernen faller gjennom alfa-, beta- og gamma-forfall, kan de ikke gjennomgå samme forfallsprosess igjen. Antallet av radioaktive kjerne i prøven minsker eksponentielt.
De aktivitet, eller forfallshastighet,er frekvensen for endring av antall radioaktive kjerner. Dette er gitt av,

Det negative tegnet betyr at antall radioaktive kjerne i en prøve er minkende over tid. $ latex \ lambda & s = 1 $ kalles forfall konstant. Det gir sannsynligheten for at en gitt kjernen vil forfall per tidsenhet. Forfallskonstanten har en spesifikk verdi for en hvilken som helst kjernekraftprosess. Jo høyere  , jo høyere sannsynligheten for forfall og antall radioaktive kjerne i prøven minsker raskere.
, jo høyere sannsynligheten for forfall og antall radioaktive kjerne i prøven minsker raskere.
Hvis antall radioaktive kjerne i en prøve om gangen  er
er  , så antall radioaktive kjerner
, så antall radioaktive kjerner  i prøven etter en tid
i prøven etter en tid  er gitt av:
er gitt av:

Antallet av radioaktive kjerne i prøven minker eksponensielt. Halvt liv ( ) Er mengden tid tatt for antall radioaktive kjerner i tiden som skal halveres. Hvis vi tegner en graf av hvordan antall radioaktive kjerne i prøven varierer over tid, får vi følgende graf:
) Er mengden tid tatt for antall radioaktive kjerner i tiden som skal halveres. Hvis vi tegner en graf av hvordan antall radioaktive kjerne i prøven varierer over tid, får vi følgende graf:

Slik beregner du Half Life - Radioactive Decay Curve
Slik beregner du aktivitet
Aktiviteten til prøven er proporsjonal med antall radioaktive kjerne tilstede. Så, vi kan lage en tilsvarende setning,

hvor  er aktiviteten til prøven til tider
er aktiviteten til prøven til tider  , med
, med  aktiviteten når
aktiviteten når  .
.
Hvis en graf av aktivitet vs tid er tegnet, vil den produsere en graf med samme form (dvs. aktiviteten avtar også eksponentielt).
Aktiviteten måles med SI-enheten becquerel (Bq). En aktivitet på 1 Bq tilsvarer en hastighet på 1 forfall per sekund. De curie (Ci) er en annen enhet brukt til å måle aktivitet. 1 Ci = 3,7 x 1010 Bq.
Half Life Formula
Vi vil nå utlede en formel for å få halveringstiden fra forfallet konstant. Vi starter med,

Etter ei stund  , antall radioaktive kjernehalvdeler. Så,
, antall radioaktive kjernehalvdeler. Så,  , eller
, eller

Med den naturlige logaritmen til begge sider får vi:

og så,

Hvordan å beregne halveringstid
Eksempel 1
Indium-112 har en halveringstid på 14,4 minutter. En prøve inneholder 1,32 × 1024 atomer av indium-112.
a) Finn forfallskonstanten
b) Finn ut hvor mange atomer Indium-112 vil bli igjen i prøven etter 1 time.
a) Siden  ,
,

b) Bruke  ,
,  atomer.
atomer.
Eksempel 2
Under behandling av skjoldbruskkreft får en pasient en prøve av jod-131 som skal inntas, som har en aktivitet på 1,10 MBq. Halvlengden av jod 131 er 8,02 dager. Finn aktiviteten til jod-131 i pasientens kropp etter 5 dagers inntak.
Vi bruker  . Først trener vi ut
. Først trener vi ut  :
:

Deretter,
 MBq.
MBq.
Merk:
- Vi regnet direkte forfallskonstanten per dag og holdt halveringstid også i dager. Så dagene avbrutt da vi beregnet
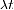 og det var ikke nødvendig å konvertere tider til sekunder (det ville ha fungert også, men det ville ha medført litt mer beregning)
og det var ikke nødvendig å konvertere tider til sekunder (det ville ha fungert også, men det ville ha medført litt mer beregning) - I virkeligheten vil aktiviteten være mindre. Dette skyldes at det også er en biologisk halveringstid knyttet til aktiviteten. Dette er frekvensen som pasienten utskiller radioaktive kjerner fra kroppen deres.
Eksempel 3
Beregn halveringstiden til en radioaktiv isotop hvis aktivitet reduseres med 4% over 1000 år.
4% = 0,04. Vi har nå
 . Ta ln på begge sider,
. Ta ln på begge sider,
 per år.
per år.
 216 år.
216 år.
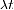 og det var ikke nødvendig å konvertere tider til sekunder (det ville ha fungert også, men det ville ha medført litt mer beregning)
og det var ikke nødvendig å konvertere tider til sekunder (det ville ha fungert også, men det ville ha medført litt mer beregning)