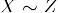Forskjellen mellom lik og ekvivalent
 Share
Share
Hovedforskjell - Like vs. Ekvivalent
Lik og tilsvarende er termer som ofte brukes i matematikk. De hovedforskjell mellom likeverdige og ekvivalente er det begrepet lik refererer til ting som ligner på alle sider, mens begrepet tilsvarende refererer til ting som ligner på et bestemt aspekt. Legg merke til at i sett teori, ordene "like" og "ekvivalent" har spesifikke betydninger, som vi vil se nedenfor.
Hva betyr likeverdig
Generelt er to ting like om de er like i alle henseender.
Når det gjelder settteori, er to sett like om de begge inneholder de samme elementene. De rekkefølge der de er oppført i et sett, spiller ingen rolle. Anta for eksempel
 og
og
 deretter,
deretter,
settet  er lik settet
er lik settet  .
.
Hva betyr ekvivalent
To ting kan sies å være likeverdige hvis de er like under en bestemt tilstand. Derfor, om to enheter er tilsvarende i stor grad avhenger på betingelse vi bruker til å beskrive deres ekvivalens. For eksempel er tallene 2 og 7 ekvivalente i den forstand at de begge er primære tall. Men hvis tilstanden vi er interessert i, er å finne ut om tallene er like, så er i denne forstand 2 og 7 ikke tilsvarende. Vi bruker symbolene  eller
eller  å indikere det
å indikere det  og
og  er ekvivalente.
er ekvivalente.
Når et kriterium er definert, tilfredsstiller ting som er likeverdige ekvivalensforhold:
- refleksivitet:
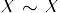
- SymmetryHvis
 , deretter
, deretter 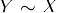
- Transitivitet: Hvis
 og
og 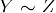 , deretter
, deretter 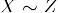
I settteori er to sett tilsvarende hvis de har samme antall elementer. Elementene selv trenger ikke å være det samme heller, bare antall elementer må være det samme. Anta for eksempel
 og
og
 deretter,
deretter,
settene  og
og  er ekvivalente.
er ekvivalente.

Symboler for å uttrykke likestilling og ekvivalens
Forskjellen mellom lik og ekvivalent
Generell betydning
Når to ting er lik, de er like i alle aspekter.
Når ting er tilsvarende, de er like i et bestemt aspekt.
I Set Theory
Når to sett er lik, de inneholder de samme elementene.
Når to sett er tilsvarende, de inneholder det samme antall elementer.
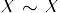
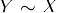
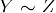 , deretter
, deretter